Tomas Mollerの交差判定【基礎編】
前回は三角錐を使った交差判定でしたが、今回はTomas Möllerのアルゴリズムという数学的な交差判定について書いてみます。これは連立方程式を機械的に解くクラメルの公式を利用して判定します。この方法の利点は平面式を使うことなく交点を求めることができ、かつコードもシンプルになります。
クラメルの公式とは
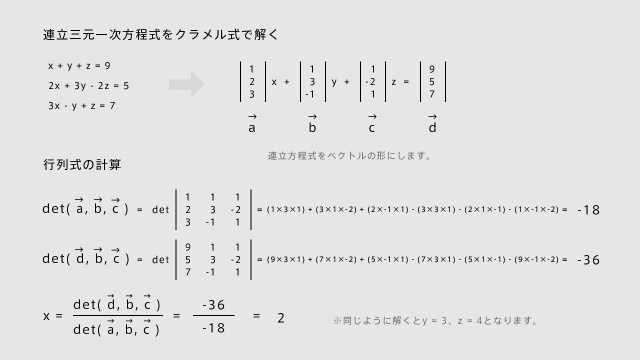
x + y + z = 9
2x + 3y – 2z = 5
3x – y + z = 7
たとえばこんな連立方程式があるとします。中学や高校の数学では、代入したり消去したりして解を求めたと思います。クラメルの公式を使うとそんな面倒なことをせずとも係数だけを使って解くことが出来ます。(クラメルの公式についてはここに解説を書いてみました)
さきほどの連立方程式にクラメルの公式を使うと、次のような流れで解くことが出来ます。上の図を参考にしながら流れを追ってみてください。(ちなみに行列式は何を計算しているかというと、3つのベクトルが成す平行六面体の体積を計算しています。)
手動で計算すると大変ですが、コンピュータに計算させれば一瞬で解答を得られますね!
交差する線分と三角形をクラメル式で解ける形にする
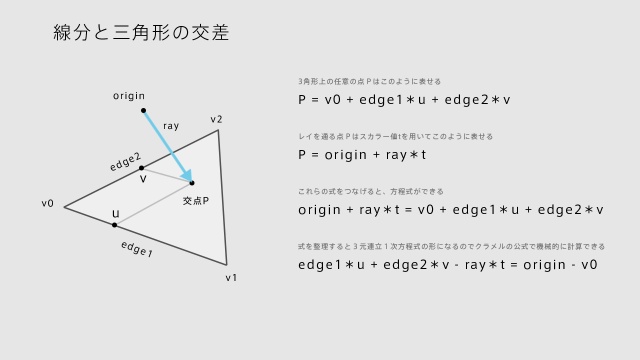
交差させるレイ(線分)と三角形をクラメルの公式で解ける形にします。レイのベクトルと原点、三角形の2辺のベクトルを使って連立方程式を作ります。
上の図の変数の型について補足:
Vector3: P, v0, edge1, edge2, origin, ray
Scalar: u, v, t
まずはレイを通る交点を直線式で表します。
P = origin + ray * t
Pは交点座標、originはレイの座標、rayは方向ベクトル、t はスカラー値となりますね。
もうひとつは三角形上の交点をエッジのベクトルで表します。
P = v0 + edge1 * u + edge2 * v
voは三角形の頂点座標、edge1は座標v1からv0を引いたベクトル、edge2も同じ要領で座標v2からv0を引いたベクトル。点Pはv0からベクトルedge1方向にu(スカラー値)、edge2方向にvだけ進んだ場所にあることになります(仮にu=1でv=0ならv1の座標にたどり着きます)。
この2つの式をつなげると、連立方程式になります。
origin + ray * t = v0 + edge1 * u + edge2 * v
整理すると
edge1 * u + edge2 * v – ray * t = origin – v0
となります。
クラメルの公式で計算する
ここでクラメルの公式を使うことになります。
x, y, zをu, v , t に置き換えてみると、係数a, b, c, dはそれぞれedge1, edge2, -ray, (origin – v0)となりますね。
公式を使って機械的に計算するだけでu、v、t の値を得ることができます。
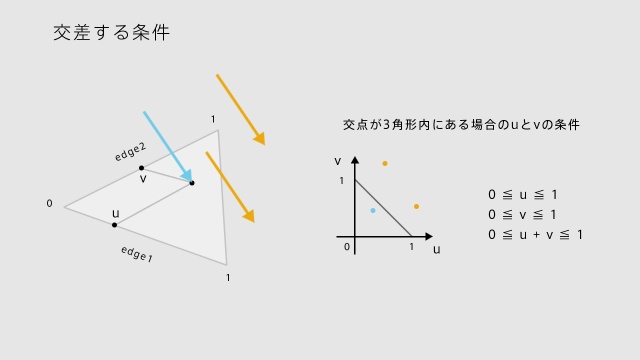
uとvの値が得られたので、この値から線分が三角形と交差しているか調べます。
三角形のuとvは一次方程式のy = -x + 1(またはy + x = 1)のグラフになるので、レイが3角形を通過するのならこのグラフ内に収まることになります。つまりuとvがそれぞれ0以上1以内でかつu+v が1以下であるなら通過しているとみなします。
参考に交差判定の関数をMayaのスクリプトで書いてみたものです。説明した通りの流れで平坦に書いてみました。割り算を回避したり、重複した掛け算を省略すればさらに速くなるはずです。
参考資料
クラメル式については詳しく書きませんでしたが、図形的に理解したいのならばこの本がおすすめです。1章の内容がベクトルとはから始まり、行列式を経てクラメルの公式を解説しています。
「ゼロから学ぶ線形代数」
http://www.amazon.co.jp/gp/product/4061546538


三角形の座標の与え方が右手系か左手系かに注意すること、と一言ほしい。