Tomas Mollerの交差判定【最適化編】
前回のつづきで、今回はTomas Möller氏の交差判定のコードについて解説してみます。ちなみにこの交差判定法は一般的に最速とされているようです。
これがコードです。このコードを解説する形で進めていきます。
前回は書きませんでしたが、自分がこの交差判定に遭遇したのは戦車ゲームにコリジョンを入れようとMicrosoftが公開しているXNAのサンプルを覗いたときでした。コードを読んでも意味がわからなかったのですが、理解せずに使うのも気持ちが悪かったのでちょっと勉強してみることにしました。ご本人の資料が公開されているので、ここを読めば詳しく書いてあります。ちなみに前回書いたものは資料に説明されていた概念に沿ってそのまま書いたものです。実際のコードは最適化されていて、計算式を変化させて重複する掛け算の省略と割り算の回避がされています。その仕組みを知らないでコードを見ても何をしているかさっぱり・・・なわけです。
では前回の連立方程式からの続きです。
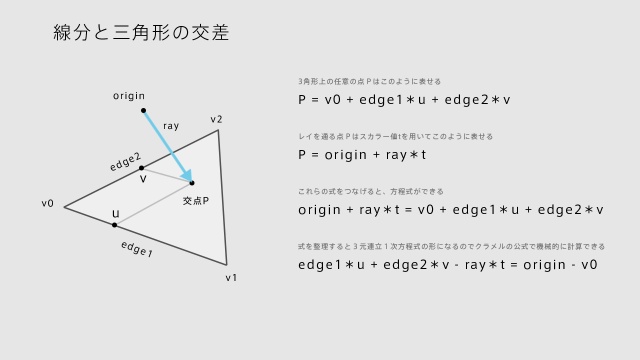
origin + ray * t = v0 + edge1 * u + edge2 * v
これを整理すると
– ray * t + edge1 * u + edge2 * v = origin – v0
ここで、分かりやすくするために以下のように表記します。
T = origin – v0
R = ray
E1 = edge1
E2 = edge2
そうするとこうなります。
-R*t + E1*u + E2*v = T
クラメルの公式からt, u, v は以下のようになります
t = det( T, E1, E2) / det( -R, E1, E2)
u = det(-R, T, E2) / det(-R, E1, E2)
v = det(-R, E1, T) / det(-R, E1, E2)
ここで行列式と外積の性質を使って式を変換します。
①行列式の値は2つのベクトルの外積と1つのベクトルの内積になることを利用 det(a, b, c) = (a x b) · c
②外積の順序の入れ替え(交換の法則) a x b = -b x a
これらを利用して行列式を内積と外積に変換するとこうなります
t = (T x E1) · E2 / (R x E2) · E1
u = (R x E2) · T / (R x E2) · E1
v = (T x E1) · R / (R x E2) · E1
(T x E1)と(R x E2)が重複することになるので、
P = (R x E2)
Q = (T x E1)
と置き換えると
t = Q · E2 / P · E1
u = P · T / P · E1
v = Q · R / P · E1
となります。PやQをあらかじめ計算しておけば後で何度も同じ掛け算をしなくて済みますよね。
今回もMaya のスクリプトで平易に書いてみました。